Nederlands Tijdschrift voor Natuurkunde

In 2004 slaagden Andre Geim en Konstantin Novoselov er als eersten in om uit grafiet één enkele laag grafeen te isoleren. Het onderzoek naar tweedimensionale nanomaterialen heeft sindsdien een hoge vlucht genomen. Naast grafeen bestaat inmiddels een breed scala aan tweedimensionale materialen die uit andere elementen dan koolstof bestaan. Mangaanoxide is een in dat verband veelbelovend transitiemetaaloxide. MnO-nanolagen met een dikte van slechts 1 nanometer kunnen inmiddels al worden gemaakt [1]. Het is experimentatoren tot nu toe echter nog niet gelukt om MnO ook als een enkele laag van slechts één atoom dik te verkrijgen. In dit artikel zal de vraag worden beantwoord of atomair vlak MnO überhaupt wel zelfstandig kan bestaan.

Heleen van Gog studeerde technische natuurkunde aan de TU Delft. Momenteel is zij gastonderzoeker aan de Universiteit Utrecht, waar zij in de onderzoeksgroep Soft Condensed Matter onderzoek doet naar nanomaterialen in het kader van een buitenpromotie.

Transitiemetaaloxides hebben unieke eigenschappen die hun oorsprong vinden in de d-elektronen van de transitiemetalen. De orbitalen van deze elektronen kunnen geheel of gedeeltelijk gevuld zijn. Transitiemetaalatomen kennen daardoor verschillende valentietoestanden en kunnen in wisselende verhoudingen bindingen met zuurstof aangaan. Polymorfisme, waarbij de verhouding met zuurstof dezelfde is maar structuren kristallografisch verschillen, behoort daarbij ook nog eens tot de mogelijkheden. De d-elektronen in transitiemetaaloxides zijn ook dikwijls ongepaard en geven dan aanleiding tot allerlei magnetische effecten. De sterke correlatie tussen de d-elektronen kan daarnaast leiden tot natuurkundige verschijnselen als de metaal-isolatortransitie, waarbij een transitiemetaaloxide van een metaal in een isolator verandert.

Hun enorme veelzijdigheid maakt dat transitiemetaaloxides materialen zijn die heel diverse toepassingen kennen. Met de huidige populariteit van tweedimensionale materialen is het niet verwonderlijk dat er ook veel onderzoek naar tweedimensionale transitiemetaaloxides plaatsvindt. Dat een transitiemetaaloxide ook als een atomair vlakke structuur zal kunnen bestaan, is echter niet vanzelfsprekend.

Berekeningen zijn uitermate geschikt om inzicht te krijgen in de stabiliteit en andere eigenschappen van nog niet bestaande structuren. Zo werden allerlei eigenschappen van het in 2004 voor het eerst gesynthetiseerde grafeen, waaronder het massaloze gedrag van de elektronen, al in 1947 aan de hand van berekeningen door Wallace voorspeld [2]. In dit artikel zullen verschillende nog niet bestaande tweedimensionale MnO-structuren met behulp van quantummechanische simulaties worden onderzocht.

DFT-berekeningen
Iedere quantummechanische benadering van een systeem neemt uiteraard de Schrödingervergelijking van dat systeem als vertrekpunt. De oplossing van deze vergelijking, de golffunctie, geeft toegang tot alle eigenschappen van het systeem. In de praktijk zijn systemen vanwege het aantal deeltjes al gauw te complex en kan de Schrödingervergelijking niet exact worden opgelost. Dat geldt ook voor de hier onderzochte MnO-structuren.

Om materialen toch quantummechanisch te kunnen doorrekenen worden daarom een aantal aannames gedaan. Omdat de elektronen vele malen sneller bewegen dan de atoomkernen, kunnen de kernen als stilstaand worden beschouwd. Dit is de zogenoemde Born-Oppenheimer-benadering. De algemene Schrödingervergelijking reduceert daarmee tot een Schrödingervergelijking voor alleen de elektronen. De interactie van de elektronen met de atoomkernen wordt daarbij opgevat als een externe potentiaal (ν_ext).

Uit de Hohenberg-Kohntheorema’s volgt bovendien dat er een een-op-eenverband bestaat tussen de elektronendichtheid en de elektronische golffunctie van een systeem dat in de grondtoestand verkeert. Ook de elektronendichtheid zal dus toegang geven tot alle eigenschappen van een systeem. Dit vereenvoudigt de berekeningen aanzienlijk. De dichtheid wordt immers alleen voor punten in de ruimte berekend en niet ook per individueel elektron bekeken. De elektronendichtheid kent daardoor slechts drie vrijheidsgraden.

Een oplossing voor de elektronendichtheid kan worden verkregen met behulp van de Kohn-Shamvergelijkingen. Het fysische systeem van elektronen die onderling Coulombafstoting, uitwisseling (exchange) en correlatie vertonen, wordt dan vervangen door een fictief systeem van elektronen dat geen interacties kent maar wel correct de elektronendichtheid van het echte systeem beschrijft. Daardoor wordt voor ieder elektron een onafhankelijke Schrödingervergelijking verkregen. De quantummechanische effecten van exchange en correlatie worden daarbij door één enkele exchange-correlatiepotentiaal (ν_xc) beschreven die een functie (functionaal) is van de elektronendichtheid.

Dit alles bij elkaar vormt de basis voor de dichtheidsfunctionaaltheorie (DFT). De elektronendichtheid en de functionaal voor de energie spelen daarin een centrale rol. Figuur 1 illustreert het stroomschema voor DFT-berekeningen. Gezocht wordt naar een oplossing voor de elektronendichtheid ρ(r) van een bepaald systeem. Binnen het onderzochte systeem ondervinden de elektronen een effectieve potentiaal ν_eff(r). Deze effectieve potentiaal kan worden berekend en is een belangrijk onderdeel van de Schrödingervergelijkingen (de Kohn-Shamvergelijkingen). Het oplossen van die vergelijkingen resulteert in golffuncties Ψ_i(r) aan de hand waarvan ρ(r) kan worden berekend. De effectieve potentiaal is op zijn beurt echter een functie van ρ(r). De oplossing voor de elektronendichtheid zal dus iteratief moeten worden gevonden. Daarbij zal met iedere gevonden ρ(r) de effectieve potentiaal weer veranderen en weer tot een andere ρ(r) leiden totdat zelfconsistentie wordt bereikt. De gezochte oplossing is de elektronendichtheid die de totale energie van het systeem minimaliseert.

Figuur 1. Iteratieschema voor DFT-berekeningen.

Doordat DFT gebaseerd is op elektronendichtheden, kunnen met behulp van dit soort berekeningen ook elektronische en magnetische eigenschappen worden onderzocht.

AIMD-simulaties
Systemen die een temperatuur hoger dan 0 kelvin hebben en waarin de atoomkernen dus niet stilstaan maar juist bewegen, kunnen met behulp van ab initio moleculaire dynamica (AIMD) worden bestudeerd. Bij AIMD draait het erom de klassieke Newtoniaanse bewegingsvergelijkingen voor de atoomkernen op te lossen. De krachten op de atoomkernen door de elektronen worden daarbij met behulp van DFT quantummechanisch berekend en dus rechtstreeks van de elektronen afgeleid. Dat maakt AIMD-berekeningen veel nauwkeuriger dan methodes die gebruikmaken van empirische modellen, maar ook veel zwaarder. De AIMD-simulaties die in dit artikel worden beschreven, werden dan ook op de nationale supercomputer Cartesius uitgevoerd (zie detailopname op de openingspagina).

Energetische stabiliteit
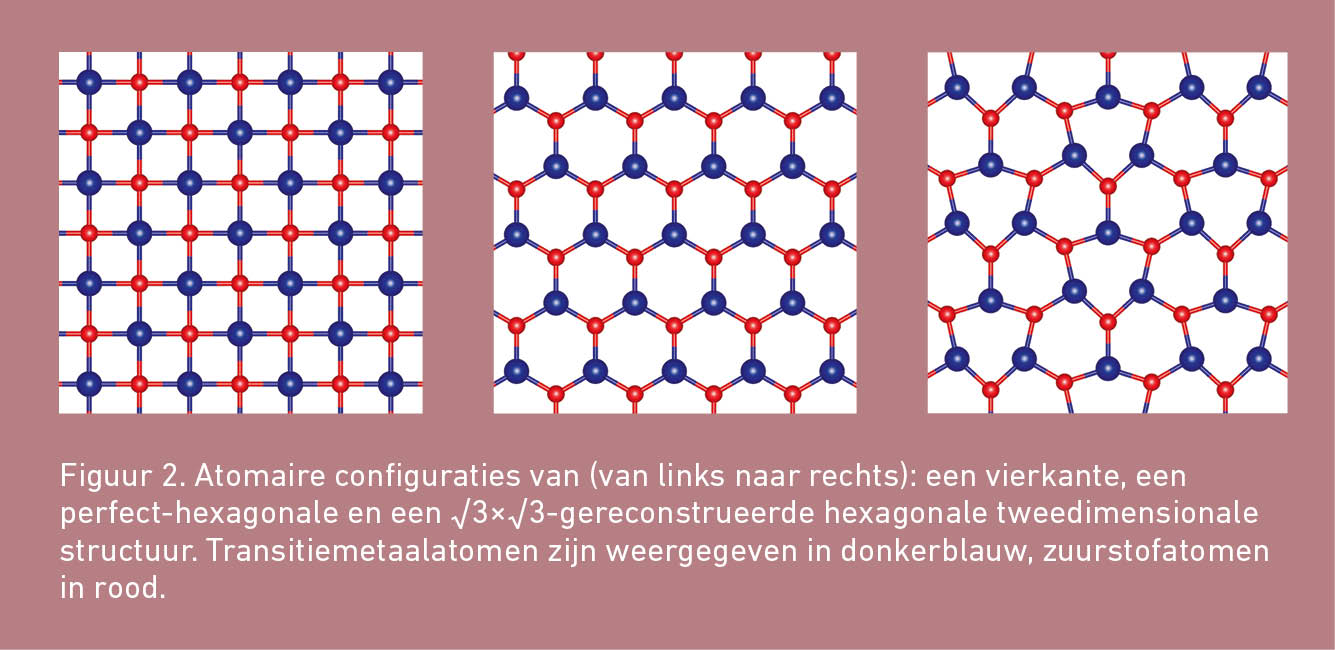
MnO neemt in de bulkfase bij voorkeur een kubische kristalstructuur aan. De in de inleiding genoemde MnO-nanolagen bestaan eveneens uit kubisch MnO. Het ligt dan voor de hand om een tweedimensionaal kubische (oftewel: vierkante) structuur als mogelijke tweedimensionale structuur voor MnO te onderzoeken. Tegelijkertijd bestaat er ook een hexagonale bulkfase voor MnO. Veel materialen zijn als tweedimensionale structuur ook stabieler in een hexagonale vorm. Naast de vierkante structuur is daarom ook naar een hexagonale MnO-fase met een perfecte honingraatstructuur als van grafeen gekeken. Een illustratie van deze tweedimensionale structuren kan in figuur 2 worden gevonden. Welke van de twee voor MnO de energetisch voordeligste structuur oplevert, is met behulp van DFT-berekeningen onderzocht.

Van transitiemetaaloxides is bekend dat de d-elektronen dikwijls ongepaard zijn. De spin van de ongepaarde elektronen van een atoom resulteert dan in een magnetisch moment op dat atoom. Vaak zijn er verschillende verdelingen van de magnetische momenten over de atomen binnen een structuur mogelijk. Deze verschillende verdelingen zullen energetisch echter meestal niet allemaal even voordelig zijn. Of de tweedimensionale MnO-structuren bij voorkeur magnetisch zijn en welke magnetische ordening in dat geval de stabielste configuratie oplevert, zal dus ook moeten worden onderzocht.

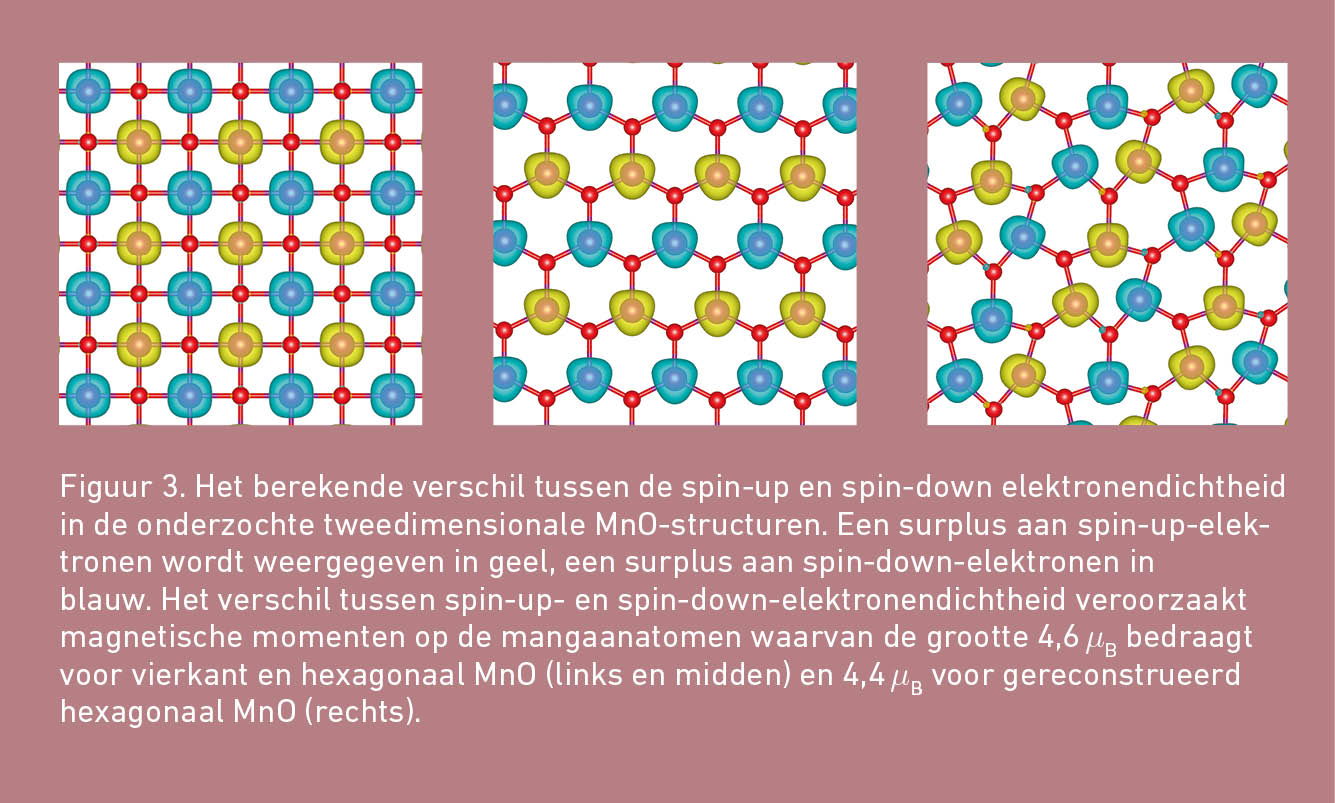
Uit de DFT-berekeningen volgt dat zowel vierkant als hexagonaal MnO energetisch het stabielst zijn wanneer de Mn-atomen een magnetisch moment bezitten. De grootte en de richting van deze magnetische momenten kan worden berekend uit het verschil van de spin-up- en de spin-down-elektronendichtheden. Daaruit blijkt dat de magnetische grondtoestand voor beide tweedimensionale structuren een antiferromagnetische ordening heeft. De magnetische momenten op de atomen zijn namelijk even groot. Zij wisselen elkaar wat richting betreft echter om en om af, zodat de structuren als geheel geen magnetisch moment hebben. Uit figuur 3 kan de precieze magnetisatie van de MnO-structuren worden afgeleid.

Wanneer we de energieën van de magnetische grondtoestanden onderling vergelijken, blijkt dat de energie van de hexagonale structuur lager is dan de energie van de vierkante structuur. Het verschil bedraagt 39 meV per atoom. Dit betekent dat hexagonaal MnO energetisch stabieler is dan vierkant MnO.

Thermische stabiliteit van vierkant MnO
Bij de berekening van de energetische stabiliteit werden de MnO-structuren verondersteld een temperatuur van 0 kelvin te hebben. Of een materiaal op hogere temperaturen stabiel is, kan met behulp van AIMD-berekeningen worden onderzocht. Hier zal voor de tweedimensionale MnO-structuren de thermische stabiliteit bij temperaturen van 300 tot 700 kelvin worden bekeken.

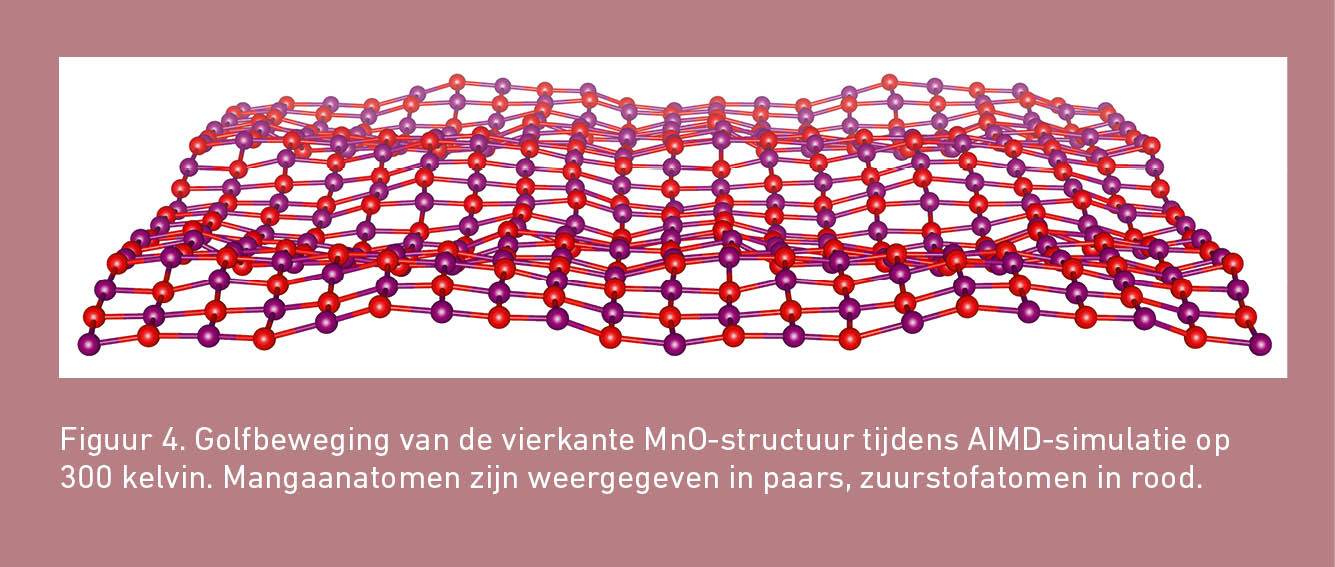
De AIMD-berekeningen laten heel mooi zien hoe de vlakke MnO-structuren beginnen te golven wanneer zij op temperatuur worden gebracht. De atomen bewegen daarbij uit het vlak en naarmate de temperatuur toeneemt, neemt ook de gemiddelde afstand tussen de atomen toe. Figuur 4 toont een illustratie van deze golfbeweging voor vierkant MnO.

Ondanks het golven breken de structuren gelukkig niet. De AIMD-simulaties laten wel een fasetransformatie voor vierkant MnO zien. Deze faseovergang vindt alleen plaats bij temperaturen vanaf 400 kelvin. Hieruit kan worden afgeleid dat er een energiebarrière bestaat voor de transformatie van vierkant MnO. Deze barrière is blijkbaar zo hoog dat bij temperaturen tot 300 kelvin de kinetische energie onvoldoende groot is om de energiebarrière binnen de tijdsduur van een AIMD-simulatie (50 picoseconden) te overwinnen. De AIMD-berekeningen laten dus zien dat vierkant MnO tot temperaturen van 300 kelvin thermisch stabiel is.

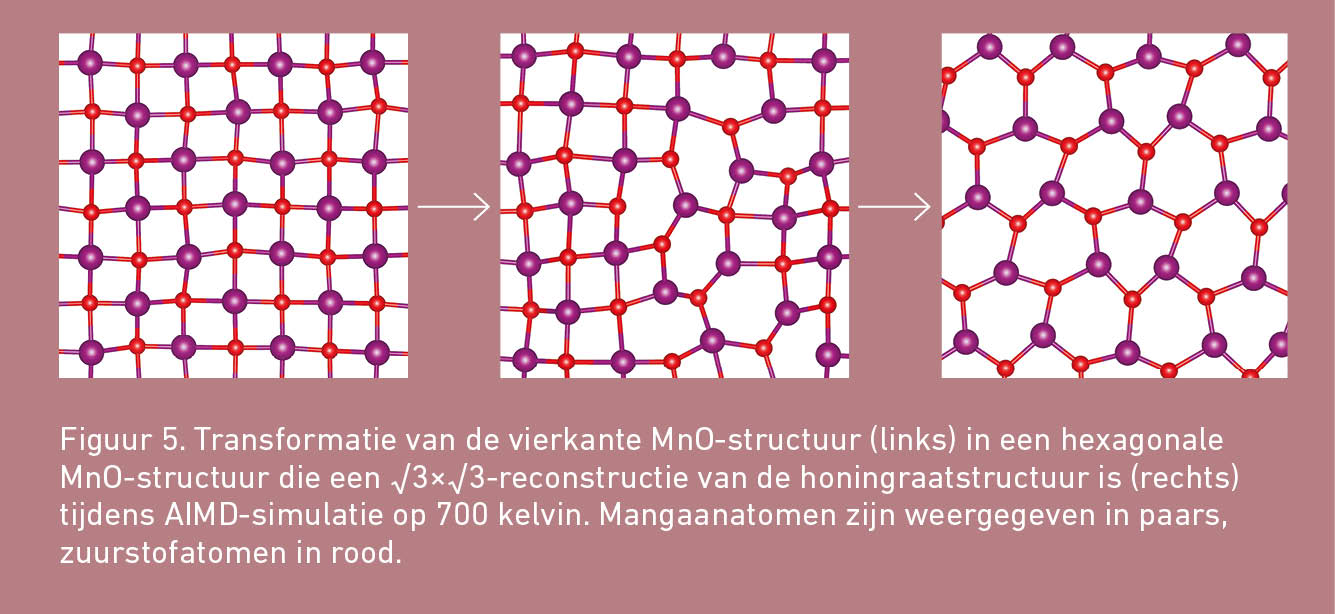
Bij temperaturen van 400 kelvin en hoger is vierkant MnO thermisch instabiel. Vierkant MnO transformeert dan in een hexagonale fase. Dat tijdens een AIMD-simulatie een fasetransformatie wordt waargenomen is behoorlijk spectaculair. Het stelt ons hier in staat om het achterliggende transformatiemechanisme te achterhalen. Zoals figuur 5 laat zien, bestaat het mechanisme eruit dat er eerst één atoombinding wordt verbroken. Daardoor ontstaat uit twee vierkanten een rechthoek met vier atomen op de hoekpunten en twee atomen in het midden van de twee lange zijden. Deze rechthoek reconstrueert vervolgens in een zeshoek.

Nieuwe hexagonale MnO-structuur
Hierboven hadden we al gezien dat hexagonaal MnO energetisch voordeliger is dan vierkant MnO. De fase waarin vierkant MnO bij hogere temperatuur transformeert, is inderdaad ook een hexagonale. Nadere analyse wijst echter uit dat het daarbij om een andere hexagonale structuur gaat dan de hierboven onderzochte honingraatstructuur.

Steeds is gecontroleerd of de structuren tijdens een AIMD-simulatie wel hun specifieke vlakke en vierkante of hexagonale karakter behielden. Na afloop van de AIMD-simulaties werden de AIMD-uitkomsten weer naar hun grondtoestand op 0 kelvin teruggebracht en vergeleken met de oorspronkelijke tweedimensionale structuren. Daaruit bleek dat de hexagonale structuur waarin het vierkante MnO transformeerde een √3×√3-reconstructie van de honingraatstructuur is. We hebben hiermee een nieuwe structuur ontdekt die nog niet eerder in de wetenschappelijke literatuur werd beschreven!

Figuur 2 illustreert hoe de nieuwe structuur eruit ziet. Door de reconstructie zijn de zeshoeken niet langer perfect hexagonaal. Waar de honingraatstructuur één vaste afstand tussen de atomen heeft, zijn dat er in de gereconstrueerde structuur twee en zijn de hoeken tussen de atoombindingen niet meer even groot. De eenheidscel van de gereconstrueerde structuur – het kleinst mogelijke patroon van atomen waarmee de complete gereconstrueerde structuur kan worden beschreven en dat zich door de hele structuur heen herhaalt – bevat ook √3×√3 (oftewel: drie) keer zo veel atomen als de eenheidscel die nodig is om de perfect hexagonale structuur te beschrijven.

Ook de hexagonale MnO-fase met een honingraatstructuur bleek tijdens AIMD-simulatie in deze nieuwe fase te reconstrueren en wel bij alle gesimuleerde temperaturen. MnO met een honingraatstructuur is dus thermisch instabiel. Dat geldt in ieder geval voor het hier gesimuleerde temperatuurinterval van 300 tot 700 kelvin. Ook buiten dat interval is thermische stabiliteit echter niet heel waarschijnlijk.

Wél thermisch stabiel tot temperaturen van tenminste 700 kelvin is de nieuw ontdekte √3×√3-gereconstrueerde hexagonale MnO-structuur. Aanvullende DFT-berekeningen laten zien dat deze structuur in zijn magnetische grondtoestand antiferromagnetisch geordend is. De √3×√3-gereconstrueerde hexagonale MnO-structuur is 71 meV per atoom voordeliger dan de hexagonale MnO-fase die een honingraatstructuur heeft.

Potentiële toepassingen
Op basis van de AIMD-resultaten kan worden geconcludeerd dat MnO inderdaad als zelfstandige atomair vlakke laag kan bestaan. Zowel een gereconstrueerde hexagonale als een vierkante fase werden thermisch stabiel bevonden. Experimenten zijn uiteraard nodig om deze thermische stabiliteit te bevestigen.

Aanvullende berekeningen voorspellen dat thermisch stabiel hexagonaal MnO een halfgeleider met een bandkloof (band gap) van 1,7 eV is. De elektronische structuur van metastabiel vierkant MnO is die van een semimetaal. Dat ze tegelijkertijd magnetisch zijn, maakt deze materialen bijzonder interessant voor toepassingen op het gebied van elektronica en spintronica. Zeker als eenmaal uit experimenten blijkt dat deze tweedimensionale materialen daadwerkelijk kunnen worden gemaakt. 

Referenties
1 X. Xiao et al., Scalable Salt-Templated Synthesis of Two-Dimensional Transition Metal Oxides, Nature Commun. 7, 11296 (2016).
2 P. R. Wallace, The Band Theory of Graphite, Phys. Rev. 71, 622 - 634 (1947).